Every Computer Programmer must understand Signed and Unsigned Numbers and its significance. Positive numbers are represented as unsigned numbers. So we don’t need to use +ve sign in front of them. However, when it comes to negative numbers we use –ve sign. This shows that number is negative and different from positive unsigned value. This is why it’s represented as signed numbers.
In Number System we’ve assumed, we have as many bits as needed to represent numbers. But in computers, we have a fix number of bits to represent value. These bit sizes are typically 8-bit, 16-bit, 32-bit, 64-bit. These sizes are usually multiple of 8, because system memories are organized on an 8-bit byte basis. When a specific number of bits being used to represent a number. This number determines the range of possible values that can be represented. For example, there are 256 possible combinations of 8-bits, therefore an 8-bit number can represent 256 distinct numeric values and the range is typically considered to be 0-255 (we have provided table in later part of this tutorial). So we can’t represent numbers larger than 255 using 8-bit number. Similarly, 16 bits allows a range of 0-65535.
Signed and Unsigned Numbers
Until now we have only considered positive values for binary numbers. When a fixed binary number is used to hold positive values, it is considered as unsigned. In this case, the range of positive values that can be represented is from 0 – 2n-1, where n is the number of bits being used. It is also possible to represent signed (negative as well as positive) numbers in binary. In this case, some part of the total range of values is used to represent positive values, and the remaining of the range is used to represent negative values.
There are several ways we can represent signed numbers in binary, but the most common representation used is called two’s complement method. The term two’s complement is somewhat ambiguous, in that it is used in two different ways. First, as a representation, two’s complement is a way of interpreting and assigning meaning to a bit pattern contained in a fixed precision binary quantity. Second, the term two’s complement is also used to refer to an operation that can be performed on the bits of a binary quantity. As an operation, the two’s complement of a number is formed by inverting all of the bits and adding 1 to it. In a binary number being interpreted using the two’s complement representation, the high order bit of the number indicates the sign. If the sign bit is 0, the number is positive, and if the sign bit is 1, the number is negative. For positive numbers, the rest of the bits hold the true magnitude of the number. For negative numbers, the lower order bits hold the magnitude of the number. It is important to note that two’s complement representation can only be applied to fixed precision quantities, that is, quantities where there are a set number of bits.
The 2’s complement method of representation is used because it reduces the complexity of the hardware in the ALU (arithmetic-logic unit) of a computer’s CPU. Using a 2’s complement method, all of the arithmetic operations can be performed by the same hardware whether the numbers are considered to be unsigned or signed. The bit operations performed are identical; the difference comes from the interpretation of the bits. The interpretation of the value will be different depending on whether the value is considered to be unsigned or signed.

The table below shows counting sequence for an 8-bit binary number using 2’s complement:
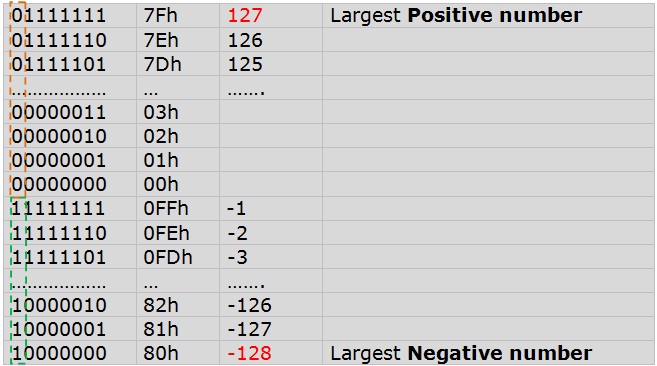
In above table, we’re counting up from 0. When 127 reached, the next binary pattern in the sequence corresponds to -128. The values from the largest positive number to the largest negative number, but that the sequence is as expected after that. Say for example, adding 1 to –128 gives –127. When the count has progressed to FFh (or the largest unsigned magnitude possible) the count wraps around to 0. Say for example adding 1 to –1 gives 0. This is it for Signed and Unsigned Numbers in computer programming. If you have any question, then feel free to leave a comment.
 BINARYUPDATES.COM EMBEDDED SYSTEMS TRAINING
BINARYUPDATES.COM EMBEDDED SYSTEMS TRAINING
