In previous post, we have seen concept, construction and working of capacitor as DC voltage source. This post is about How Capacitor Works with DC. The capacitors are widely used in DC electronics. The questions come in mind when we think about DC and capacitor are,
- How capacitor works with DC input?
- What is the final voltage of capacitor after getting charged?
- How much time capacitor takes to charge/discharge?
Let’s discuss about solution to above questions.
How Capacitor Works with DC
Capacitor performs three tasks in dc circuits i.e. taking charge, holding charge and delivering charge at certain time. When capacitor is connected to dc voltage source, capacitor starts the process of acquiring a charge. This will built up voltage across capacitor. Once capacitor has acquire enough charge, current starts flowing and soon capacitor voltage reaches at value approximately equal to dc source voltage. When capacitor has almost full voltage across it, no more current flows though capacitor. This take some time. But there is an interesting fact. The capacitor will not acquire 100% charge at same instant when dc voltage is given to it. The capacitor gets first part of total charge quickly, second part slowly, third part more slowly and so on. Hence we can say that capacitor charges non-linearly.
You can imagine this situation with bus analogy. Compare bus with capacitor, vacant seat with space and people with electrons. In bus, every person try to acquire a seat. If fewer seats remaining, people need more time to find vacant seat. Similarly, electrons try to acquire space on plate of capacitor. Here, electrons require some time to get on plates. Rewind the construction of capacitor. For input dc voltage, first plate charges to input voltage. As there is no conducting path in between two plates, second plate take some time to get charge.
This time defines charging time of capacitor. So, we need to find out parameters on which charging time of capacitor depends. According to ohms law, if circuit resistance is increased, less current is available to charge a capacitor. This increases time require for capacitor to charge. As capacitance and voltage are inversely proportional to each other, increase in value of capacitance takes a longer time for capacitor to charge itself. So, with these relations we can say that the charging time of capacitor depends on both resistance of circuit and capacitance of capacitor. This is time constant of capacitor. But, the process of measuring charging time of capacitor is complex, since capacitor will never charge at same rate.
The charging time or time constant is denoted as τ (tau). It defines time taken by capacitor of “C” farads in series with resistance of “R” ohms, to acquire first part of total charge. Time constant can be mathematically define as,
Charging time = Resistance x Capacitance
τ = R x C
The time constant is the time capacitor needs for either voltage or current to increase to 63.21 % of maximum or decrease to 36.79 % of initial value.
Why capacitor charges to 63% of the applied voltage?
Here is the equation for voltage across capacitor at any instant of time during charging.
Vc = Vi (1 – e-τ / RC )
Where Vc = capacitor voltage, Vi = input voltage, t = charging time, R = resistance, C = capacitance
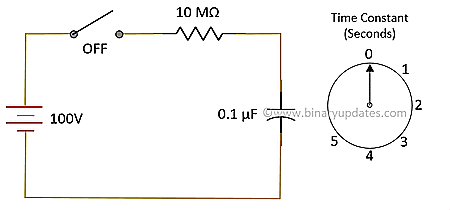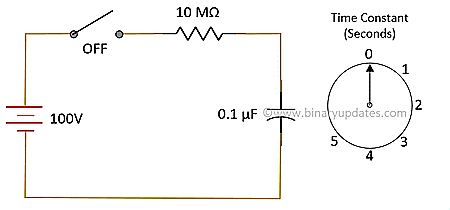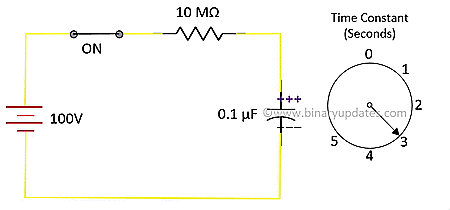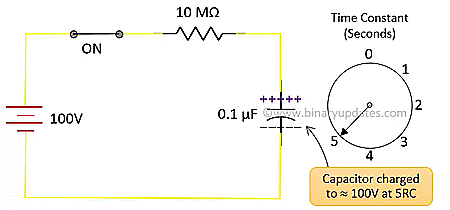
E.g. for R = 10 MΩ and C = 0.1 µF, time constant is 1 second. This doesn’t mean that capacitor will be fully charge in 1 second. It means that capacitor will be charge to 63% of input voltage in 2 seconds. If we continue to apply the voltage, capacitor takes 63% of the voltage difference between current voltage and input voltage. This process will repeat itself till capacitor acquires full charge. We get value 63% or 0.63 when we put one time constant in above equation. We can calculate current at any instance (time) in capacitor using ohms law. Consider same circuit as discussed earlier. Here is the current equation during charging of capacitor.
Ic = ( Vi – Vc ) ⁄ R
The table below shows values of capacitor charging voltage and current for respective time constant.
| Switch position | Time constant (τ) (in seconds) | Capacitor charging voltage (Vc) (in volts) | Capacitor charging current (Ic) |
| OFF | 0 | 0 | 10 µA |
| ON | 1RC | 63.2120 | 3.6787 µA |
| ON | 2RC | 86.4664 | 1.3533 µA |
| ON | 3RC | 95.0212 | 0.4978 µA |
| ON | 4RC | 98.1684 | 0.1831 µA |
| ON | 5RC | 99.3262 | 0.0673 µA |
| ON | 8RC | 99.9664 | 3.3546 nA |
| ON | 11RC | 99.9983 | 0.1670 nA |
| ON | 14RC | 99.9999 | 8.3152 pA |
| ON | 17RC | 99.9999 | 0.4139 pA |
The term 1RC, 2RC etc. defines number of times a constant voltage that must be applied to capacitor. The table above reminds important fact related to capacitor i.e. the capacitor will never store complete charge given to it. For every time constant capacitor voltage increases slowly (except first) but it will never equal to the input voltage. The current flowing through resistor capacitor circuit is decreases as time (τ) increases. Here is the graph showing behavior of charging voltage and current of capacitor.
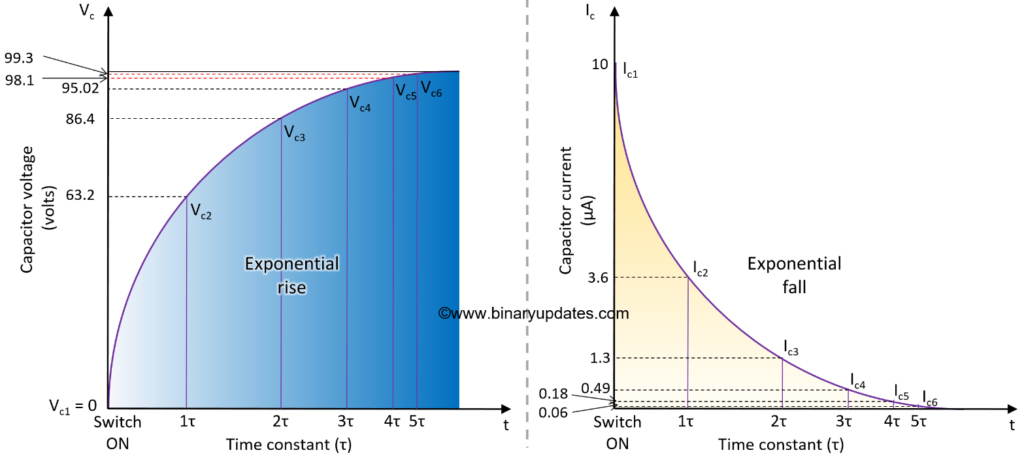
The graph of capacitor charging voltage and current is exponentially rising and falling in nature respectively. The curve shows how much time capacitor need to get almost full charge. The exponential rise of voltage and exponential decay of current in capacitive circuit is not same or it is not in phase. Note that the x axis of graph is changed with respect to value on y axis to have a clear view change in voltage or current. The graph is not as per specific scale. In 5RC seconds, charging current Ic ≈ 0 and charging voltage Vc ≈ input voltage.
Capacitor Discharging in DC Circuits
There are multiple ways to discharge a charged capacitor. The easiest way is to use LED or resistor in series with capacitor. We need to take extreme care while selecting resistor or led for capacitor to discharge. It is good practice to refer specifications like wattage, value in case of resistor and forward current, voltage in case of LED before use. The discharging circuit for capacitor is shown below.
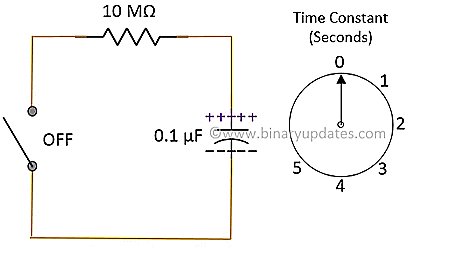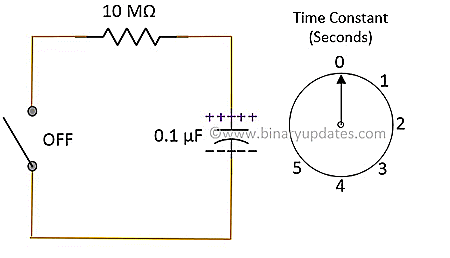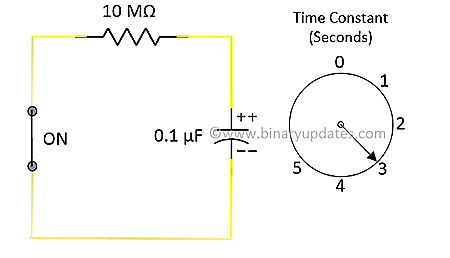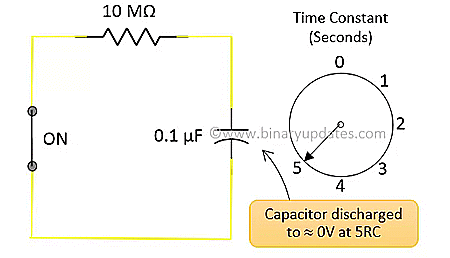
Here are the equations for voltage across capacitor and current in capacitor at any instant of time during discharging.
Vd = Vi ( e-τ / RC) Id = Vd ⁄ R
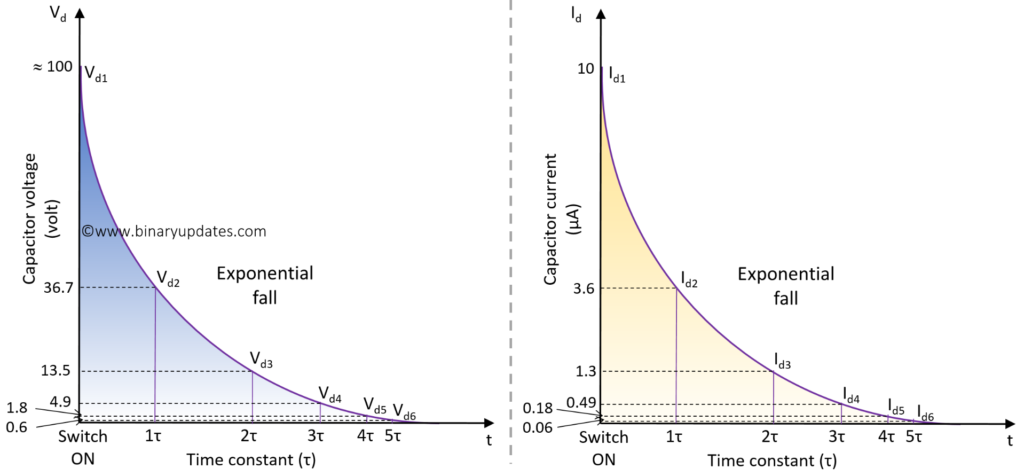
The table below shows values of capacitor discharging voltage and current for respective time constant. During discharging, the voltage from which capacitor starts discharging is last charge
| Switch position | Time constant (τ) (in seconds) | Capacitor charging voltage (Vd) | Capacitor charging current (Id) |
| OFF | 0 | ≈ 100 V | 10 µA |
| ON | 1RC | 36.7879 V | 3.6787 µA |
| ON | 2RC | 13.5335 V | 1.3533 µA |
| ON | 3RC | 4.9877 V | 0.4978 µA |
| ON | 4RC | 1.8315 V | 0.1831 µA |
| ON | 5RC | 0.6737 V | 0.0673 µA |
| ON | 8RC | 0.0335 V | 3.3546 nA |
| ON | 11RC | 1.6701 mV | 0.1670 nA |
| ON | 14RC | 30.5902 µV | 8.3152 pA |
| ON | 17RC | 4.1399 µV | 0.4139 pA |
During discharging, the capacitor voltage and current decreases quickly at 1RC second and after that there is slow decrease in both quantities. Here is the graph of capacitor discharging voltage and current. Both graphs are exponentially falling in nature. In 5RC seconds, discharging current Id ≈ 0 and discharging voltage Vd ≈ 0.
This is it for now. I hope now you know How Capacitor works with DC. In future post, we will learn about capacitor in AC circuits. Thanks for reading and don’t forget to leave a comment.
 BINARYUPDATES.COM EMBEDDED SYSTEMS TRAINING
BINARYUPDATES.COM EMBEDDED SYSTEMS TRAINING